コンクリートは、レディーミクスト工場や製品工場、現場練り、海洋工事用のプラント船など、さまざまな場所で製造されます。いずれの方法でも、経済性と所定の品質の確保が求められます。
材料の貯蔵設備と管理
セメントおよび混和材料
- 防湿構造のサイロや倉庫に種類別で保管。
- サイロ容量は1日平均使用量の3倍以上が望ましい。
- 袋詰セメントは、地上30cm以上に13袋以下で積み重ね、入荷順に管理。
骨材
- 種類・品質別に区分し、粒度分離・異物混入を防止。
- 貯蔵床は排水構造とし、凍結・乾燥・温度上昇を防ぐ。
- 軽量骨材にはプレウェッティング設備が必要。
- 貯蔵容量は1日最大使用量以上。
- 骨材の粒度・含水状態は品質に影響するため、均質供給が可能な運搬設備が必要。
混和材料
- 防湿性のあるサイロや倉庫に品種別で保管。
- 液状:分離・凍結防止
- 粉末:吸湿・固結防止

コンクリート標準示方書[施工編:施工標準]「5章 製造」で、コンクリート材料の貯蔵設備・管理について規定されています。
コンクリートの製造工程
製造設備の構成
- 材料貯蔵設備
- 材料計量設備
- 練混ぜ設備
→ バッチ計量方式+バッチミキサが基本。
(参考)バッチャープラント仕組みの画像を見る
計量と誤差
- JIS A 5308により、材料ごとの計量誤差の許容範囲が定められています。
- 計量誤差は、目標値との差を百分率で表し、小数点1位で四捨五入。
出典 JIS A 5308 :2019 及び コンクリート標準示方書2017[施工編]5.3 計量
※ JIS A 5308 :2024と同一
練混ぜと均質性
材料投入順序
- ミキサの形式、骨材の種類・粒度、配合、混和材の種類などにより異なる。
- 事前に適切な順序を定めることが必要(示方書に規定あり)。
練混ぜ時間
- 原則としてJIS A 8603-2による試験結果から決定。
- 試験を行わない場合の最小時間:
- 重力式ミキサ:1分30秒
- 強制練りミキサ:1分
均質性の目安
- モルタル単位容積質量差:0.8%以下
- 単位粗骨材量の差:5%以下

コンクリート標準示方書[施工編:施工標準]5章 コンクリートの製造 5.4 練り混ぜで、規定されています。
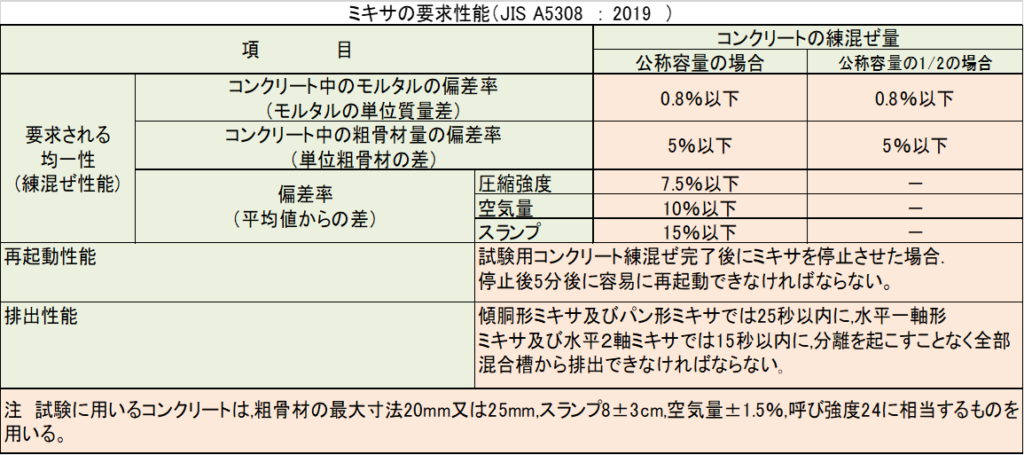
ミキサの要求性能
出典 JIS A 5308 :2019
問題(技士)

理解度を確認するために、以下の過去問題に挑戦してみましょう。
四肢択一の過去問題です。正解と思う設問の○をクリックまたはタップしてください。解き終わったら「回答」をクリックまたはタップすると解答が表示されます。
品質管理と検査
品質管理の目的
- 品質変動の抑制と異常の早期発見・是正。
- スランプ、水セメント比、圧縮強度などが特性値として用いられます。
定義(コンクリート標準示方書より)
- 品質管理:目的に合致した構造物を経済的に造るための技術活動。
- 検査:品質が基準に適合しているかを判定する行為。
特性値と物性値の違い
| 用語 | 意味 |
| 物性値 | 圧縮強度、ヤング係数、収縮ひずみなど、材料の性質を示す値 |
| 特性値 | 試験値のばらつきを考慮し、一定の確率で基準を満たすよう設定された値 |

物性値・特性値とは、どのような意味か注意しておきましょう。
コンクリートの圧縮強度、ヤング係数、収縮ひずみ、水分浸透速度係数、塩化物イオン拡散係数、相対動弾性係数等を総称して、コンクリートの物性値と呼びます。
一方特性値とは、材料物性の試験値のばらつきを想定したうえで、1回の試験値が望ましくない側に下回るか、もしくは上回る確率が一定の値となるように設定される材料物性の基準となる値を特性値と呼ぶ。
出典:土木学会:2023年制定コンクリート標準示方書【施工編】21p
2023年制定による品質管理と検査の位置づけ
コンクリート標準示方書〔施工編〕では、施工標準の13章品質管理に施工者が行う検査が記載され、示方書〔検査標準〕は、発注者が行う検査が記載されるようになりました。
管理図による工程管理
管理図の種類
- \({X}\) 管理図:個々の測定値
- \(\bar{X}\) 管理図:平均値
- \({R}\) 管理図:範囲(最大値-最小値)
- \({R_s}\) 管理図:隣接値の差(移動範囲)
→ 一般的には \(\bar{X}\)-\({R}\) 管理図が用いられます。
コンクリートの管理に用いられる管理図は、つぎのものがあります。
出典:コンクリート技術の要点’20 140P
\({X}\) 管理図(\({X}\):サンプルの特性値)
(1個の測定値をただちに打点して作図する。)
\(\bar{X}\) 管理図(\(\bar{X}\):平均値)
(数個の測定値の平均値を打点して作図する。)
\({R}\) 管理図(\({R}\):範囲(ロット内の最大値と最小値の差))
(ロット内の測定値のバラツキ(範囲)を作図する。)
\({R_s}\) 管理図(\({R_s}\):特性値と次の特性値\({X}\) との差(移動範囲))
(隣り合う(相隣る)2つの測定値の差(移動範囲)を作図する。)
一般に\(\bar{X}\)-\({R}\) 管理図、\({X}\)-\({R}\) 管理図が用いられる。
\(\bar{X}\) 管理図は品質の平均値の変化を見るためのものであり、\({R}\) 管理図は品質の幅の変化をみりためのものである。
\(\bar{X}\)-\({R}\) 管理図は工程の解析、工程の能力の検討などに有効である。
管理図の構成
- 中心線(CL):平均値
- 管理限界:±3σ(UCL/LCL)、±2σ(内側限界)
下図は、圧縮強度の 管理図(\(\bar{X}\)-\({R}\) 管理図)の一例を示しています。
中心線は平均値\({X}\) 、上方管理限界(UCL)は、[\(\bar{X}\)+3\(\sigma\)]、下方管理限界(LCL)は、[\(\bar{X}\)-3\(\sigma\)]、内側限界は[\(\bar{X}\)\(\pm\)2\(\sigma\)]としています。出典:コンクリート技術の要点’20 140P
下図は、管理図において、異常を判定する8つの判定基準(JIS Z 9020-2附属書B)が示されています。ここでは、上方管理限界(UCL)と下方管理限界(LCL)は、中心線\(\bar{X}\)から3\(\sigma\)の距離にある。以下の判定基準(ルール)を適用するために、管理図をそれぞれ1\(\sigma\)間隔で六つの領域に分ける。中心線から対称に、順次A,B,C,C,B,Aとする。
問題(技士)

理解度を確認するために、以下の過去問題に挑戦してみましょう。
四肢択一の過去問題です。正解と思う設問の○をクリックまたはタップしてください。解き終わったら「回答」をクリックまたはタップすると解答が表示されます。
正規分布と品質管理
平均値と標準偏差
特性値(コンクリートの強度やスランプなど)に関するn個のデータ\(x_i\)(\(i)\)=1,2,3,~\(n)\)があるときの平均値\(m)\)と標準偏差\(\sigma\)は以下のように計算される。
平均値
$$m = \frac{1}{n}{\displaystyle \sum_{i=1}^n x_i}=\frac{(x_1+ x_2+\ldots+x_n)}{n}$$
標準偏差
$$\eqalign{\sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (m- x_i )^2} &= \sqrt{\frac{(m- x_1 )^2+(m- x_2 )^2+\ldots+(m- x_n )^2}{n}} }$$
標準偏差は、\( x_i\) の変動の程度を表す量であり、\( x_i\) の変動の原因が全くの偶然である場合は正規分布に近似でき、コンクリートの特性値も同様に一般に以下に示す正規分布\(p(x)\)に近似出来る。
正規分布の式
\[p(x)=\frac{1}{\sqrt{2\pi \sigma^2}}\exp{\left\{-\frac{(x-m)^2}{2\sigma^2}\right\}}\]
下図が正規分布図となります。
(m-\(\kappa\))以下〔またはm+\(\kappa\)以上、m-\(\kappa\)は定数〕のデータが得られる確率は、斜線部の面積の全面積に対する割合として計算され、正規分布表として示されます。

式の中の変数はm(平均値)とσ(標準偏差)だけです。データのσ(バラツキ)が小さいと尖って、σ(バラツキ)が大きいとなだらかな曲線になるのは、直感的にわかりますよね。

度数分布が平均値\(m\)、標準偏差\(\sigma\)の正規分布になるとき、\(N(m,\sigma^2)\)をなすと書きます。
〔\(N\)は正規分布(Normal distribution)の頭文字〕
変動係数
\[V=\frac{\sigma}{m}\times100(%)\]
標本平均
通常の場合では、サンプルを抽出してデータを得、このデータのみで母集団(もととなる全体の値や性質)を推定しなければなりません。推定する方法の例がコンクリート技術の要点’20 139pに示されています。
ⅰ)\(N(m,\sigma^2)\)をなす母集団よりn個のデータを抽出してその平均値\(\bar{x}\)(標本平均という)を求めることを繰り返すと、\(\bar{x}\)は、\(N(m,\sigma^2)\)の分布をなす。すなわち標本平均の平均値は、母集団の平均値に一致し、標本平均の標準偏差は、母集団の標準偏差の\(1/\sqrt{n}\)になる。

私は、ある参考書のコンクリート配合強度を出す際の割り増しの説明で、以下の記述があったことを思い出します。
ⅰ)1回の試験結果は、購入者が指定した呼び強度の85%以上でなければならない。ⅱ)3回の試験結果の平均値は、購入者が指定した呼び強度の強度値以上でなければならない。
これを標準偏差(σ)で表すと
ⅰ)配合強度\(f’_{cr}\)=0.85\(\times\)設計基準強度\(f’_{ck}\)+3σ
ⅱ)配合強度\(f’_{cr}\)=設計基準強度\(f’_{ck}\)+1.73σ
ⅰ)の式は、3σの範囲に入らなきゃダメというのはすぐ理解できると思います。ですが、ⅱ)の式の1.73σの意味が最初、この参考書だけではわかりませんでした。丁寧に書くと以下になります。
ⅱ)配合強度\(f’_{cr}\)=設計基準強度\(f’_{ck}\)+\(3\times\)\(\frac{\sigma}{\sqrt{3}}\)
\(3\times\)\(\frac{\sigma}{\sqrt{3}}\)を計算すると1.73σになりますよね。
その時は、もうちょっとだけ丁寧に書いてくれればいいのにと思った次第です。
配合強度と不良率の関係
| 配合強度の設定 | 不良率の目安 |
| 平均値 = 目標強度 | 約 50% |
| 平均値 + 1σ | 約 16% |
| 平均値 + 2σ | 約 2.3% |
| 平均値 + 3σ | 約 0.1% |
→ 3σを管理限界に設定すれば、ほぼ不良品は出ないと考えられます。
配合強度をm(供試体強度の平均値)と不良率の関係を正規分布によって、推定することが出来ます。
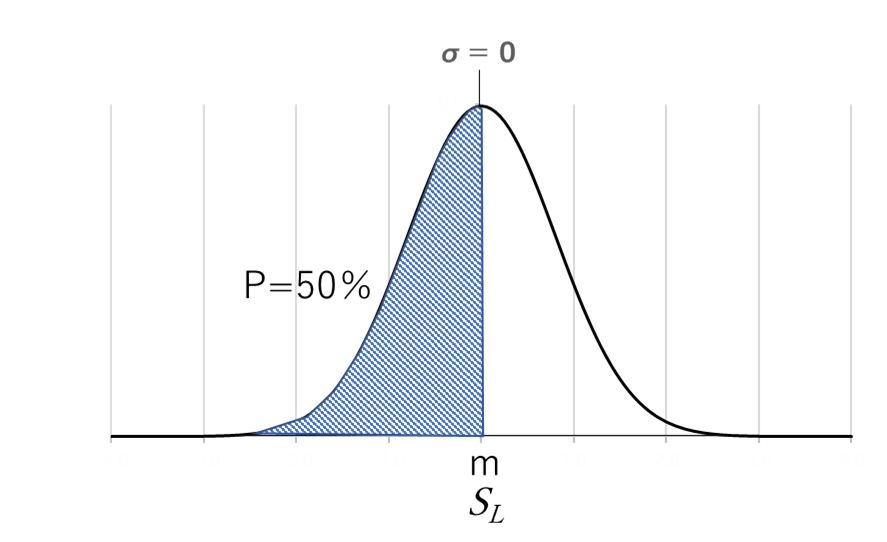
(1)配合強度mを目標強度SLとした場合、(目標強度に達しない供試体の)不良率は50%になる。
(下図の着色部分の面積が目標値SLを下回る確率となります。)
例えば、標準偏差が2.5N/mm2とし、平均強度m=21N/mm2、目標強度SL=21N/mm2の場合、供試体の半数の50%が、目標強度SL=21N/mm2を満足できなことになります。
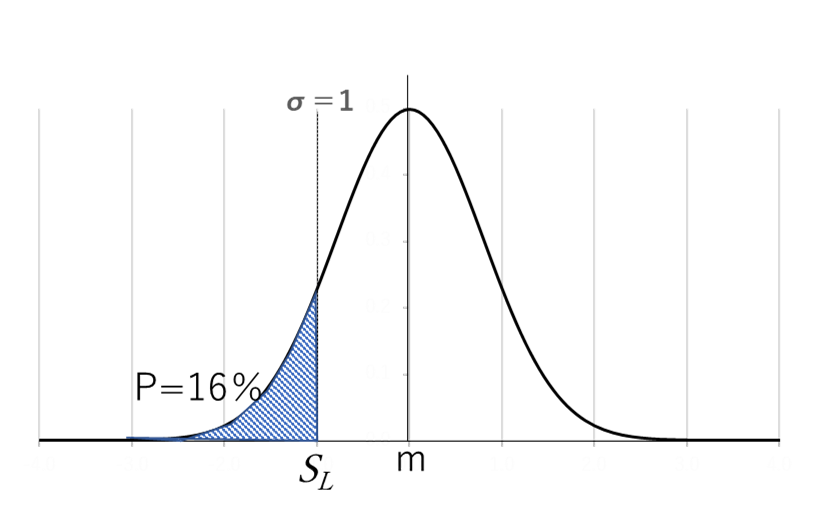
(2)配合強度mをσ=1ぶんだけ目標強度SLを大きくすると、不良率は16%になる。
目標強度を1σ上げた場合(21+2.5=23.5N/mm2)、不良率は16%となります。
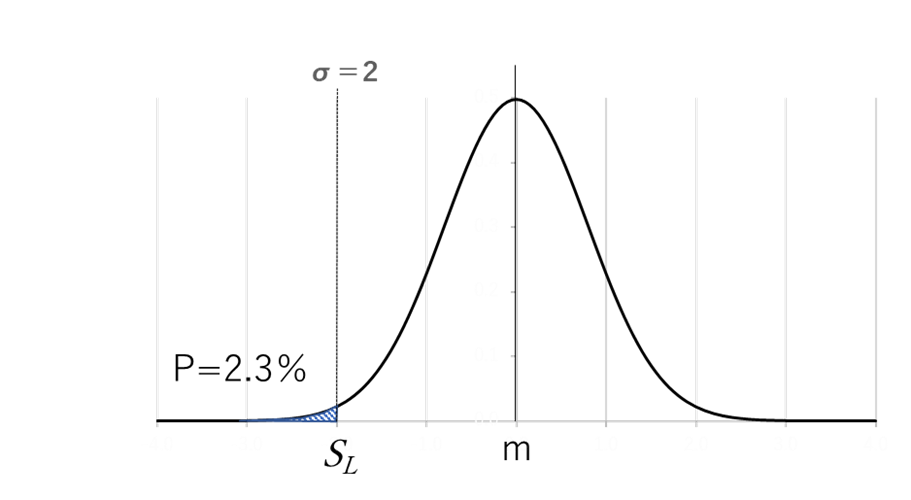
(3)配合強度mをσ=2ぶんだけ目標強度SLを大きくすると、不良率は2.3%になる。
目標強度を2σ上げた場合(21+2.5✕2=26.0N/mm2)、不良率は16%となります。
(4)配合強度mをσ=3ぶんだけ目標強度SLを大きくすると、不良率は0.1%になる。
目標強度を3σ上げた場合(21+2.5✕3=28.5.0N/mm2)、不良率は0.1%となります。


管理限界値にm+3σを用いれば、不良率が0.1%なので、ほぼ不良品は出ないと考えることが出来ます。ただし配合設計で圧縮強度の目標値を設定する場合には、JIS A 5308や土木学会コンクリート示方書、建築学会JASS 5の規定を満足し、かつ経済性にも留意する必要があります
✅ 試験対策のポイント
- 材料の貯蔵条件・計量誤差の基準を覚える
- 練混ぜ時間や均質性の判断基準を理解する
- 品質管理の定義や目的、特性値の意味を整理する
- 管理図の種類と構成、正規分布の基本式を理解する
- 配合強度と不良率の関係を図でイメージできるようにする