2023年に改訂されたコンクリート標準示方書【施工編】では、レディーミクストコンクリートの圧縮強度の目標値の定め方について、統計的な考え方がより明確に示されました。消費者危険や生産者危険などのリスクを考慮し、適切な配合強度や呼び強度を設定することが求められます。
圧縮強度の目標値の考え方
JIS認証品のレディーミクストコンクリートを購入する際、以下のような方法で呼び強度を設定することが考えられます:
- 圧縮強度の下限値(呼び強度の85%)を指定する方法
- 合格判定基準値を呼び強度に指定する方法
- 圧縮強度の特性値を呼び強度に指定する方法
標準示方書では、施工に用いるコンクリートの強度目標値が配合強度より低くならないよう、呼び強度は合格判定基準値を満足するように指定することが推奨されています。
合格判定基準値とリスクの考慮
合格判定基準値を定める際には、以下の2つのリスクを考慮する必要があります:
- 不良率(消費者危険):施工後に強度不足となるリスク
- 生産者危険:検査で不合格となるリスク
発注者によって不良率の設定は異なり、5%とする場合もあれば25%とする場合もあります。検査基準は発注者の判断に委ねられる形です。
参考文献:日本コンクリート工学会『コンクリート技士・主任技士研修テキスト’24』p65~68
圧縮強度の目標値を定める式(概要)
標準示方書では、統計的な手法を用いて圧縮強度の目標値を算出する式が示されています。以下はその概要です:
■ 試験値の平均値(1回の試験=3本の供試体の平均)
\(f’_{avg}\)=\(\frac{1}{{1-1.645V_1}}\)\(\cdot f’_{ck}\)
■ 合格判定基準値(生産者危険 \({\alpha}%\)を考慮)
\( f’_{cn} = \left(1 – \frac{K_{\alpha}V_1}{\sqrt{n}} \right) \cdot f’_{avg} \)
■ 圧縮強度の目標値(検査不合格率0.135%を考慮)
\(f’_{cr}=\frac{1}{1-3V_0/\sqrt{n}}\cdot f’_{cn}\)
■ 割増し係数(配合設計時に使用)
\(割増し係数=\frac{1}{1-3V/\sqrt{n}}\cdot\frac{1-K_{\alpha}V/\sqrt{n}}{1-1.645V}\)
※ここでの変動係数\(V\) は、標準偏差を目標値で割った値です。
設計時の参考値
試験回数 \(n=3\)
変動係数\( V=10%\)
生産者危険\({\alpha}=10%\) →\(K_{\alpha}=1.282\)
割増し係数 ≒ 1.34
出典:土木学会:2023年制定 コンクリート標準示方書【施工編】 59~60P
土木学会標準示方書

以下は、2023年制定土木学会コンクリート標準示方書【施工編】に掲載されている内容です。かなり難しい式が並んでいますが、式の暗記は私の場合不可能です。
式には、JISで定めている1回の試験値とは、3本の供試体の平均値であること、消費者危険、生産者危険が導入されている。ここがポイントだと思っています。
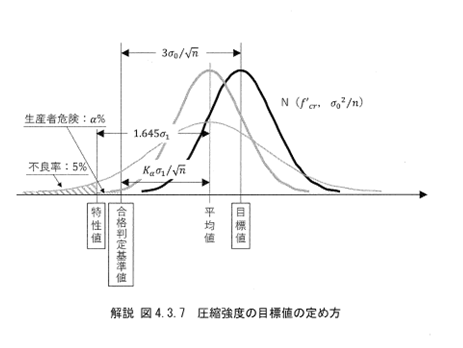
1回の試験値が特性値を満足しない確率が5%となる分布の平均値\(f’_{avg}\)は、式(解4.3.1)で表される。圧縮強度の試験値とは、同一バッチから採取される3本の供試体の圧縮強度の平均値のことである。
\(f’_{avg}\)=\(\frac{1}{{1-1.645V_1}}\)\(\cdot f’_{ck}\)(解4.3.1)
ここに\(f’_{ck}\):圧縮強度の特性値
\(V_{1}\) :変動係数(=標準偏差\(\sigma_{1}\)/平均値\(f’_{avg}\))試験回数が \(n\)回のとき、生産者危険を\(\alpha\)%とし、標準正規分布において上側確率が\(\alpha\)%となる点を\(K_{\alpha}\)とすると、合格判定基準値\(f’_{ck}\)は、式(解4.3.2)で表される。
\(f’_{cn}\)=(1-\(K_{\alpha}\) \(V_1\)/\(\sqrt{n}\))\(\cdot f’_{avg}
=\frac{1-K_{\alpha}V_1/\sqrt{n}}{1-1.645V_1}\cdot f’_{ck}\) (解4.3.2)検査に合格とならない確率を0.135%となるように圧縮強度の目標値\(f’_{cr}\)を定めると、圧縮強度の目標値\(f’_{cr}\)は、式(解4.3.3)となる。
\(f’_{cr}=\frac{1}{1-3V_0/\sqrt{n}}\cdot f’_{cn}
=\frac{1}{1-3V_0/\sqrt{n}}\cdot\frac{1-K_{\alpha}V_1/\sqrt{n}}{1-1.645V_1}\cdot f’_{ck}\) (解4.3.3)
ここに、\(V_0\) :変動係数(=標準偏差\(\sigma\)/目標値\(f’_{cr}\))変動係数\(V_0\)および\(V_1\)は等しく、\(V\)とすれば、割増し係数は、式(解4.3.4)で表される。
\(割増し係数=\frac{1}{1-3V/\sqrt{n}}\cdot\frac{1-K_{\alpha}V/\sqrt{n}}{1-1.645V}\)(解4.3.4)
ここに、\(V\) :圧縮強度の変動係数(=標準偏差\(\sigma\)/目標値\(f’_{cr}\))
\(K_{\alpha}\):検査計画書に示される生産者危険を\(V\)としたとき、標準正規分布において上側確率が\({\alpha}%\)となる点
配合設計時においては、\(n\)は3、変動係数\(V\)は、10%としてよい。また、検査計画書に示される生産者危険\({\alpha}%\)が10%の場合、\(K_{\alpha}\)は、1.282となり、割増し係数は、1.34になる。
出典:土木学会:2023年制定 コンクリート標準示方書【施工編】 59~60P
統計の重要性と参考文献

品質管理・品質検査において、統計の理解は避けて通れません。
以下の文献も参考になります:
町田篤彦”コンクリートの品質管理及び品質検査と統計の関係”コンクリート工学
(当時の基準に基づいて書かれていますので、ご留意願います。)
また、当ブログの関連記事として:
👉 第10章:コンクリートの製造と品質管理
👉 第5節:正規分布の基礎知識
もぜひご参照ください。受験対策として最低限押さえておきたい統計の知識をまとめています。



コメント